#2 - Hackeando la Quiniela
¿Es posible jugar a la quiniela de forma rentable? La respuesta es sí. Esta es la estrategia que ya estamos utilizando de forma 100% automatizada.
Índice
1. Lo primero es conocer el juego
2. Premisas clave de la metodología
3. Análisis completo para encontrar la quiniela más rentable
4. Análisis Premio Esperado VS Probabilidad de Premio
5. Implementación real a través de heurísticas
6. Resultados tras 51 jornadas probando la estrategiaA lo largo de todo el post hablaré en primera persona del plural porque toda la metodología descrita la hemos desarrollado juntos PapaFire y yo.
1. Lo primero es conocer el juego
Si conoces perfectamente el juego puedes saltarte esta sección. En caso contrario, sigue leyendo.
Los básicos
La idea es sencilla. Se presentan 15 partidos de futbol. En los 14 primeros tienes que predecir si ganará el local (1), el visitante (2) o habrá empate (X).
El objetivo es acertar el máximo números de partidos posibles.
El último partido, el 15, se llama Pleno al 15. Solo suma si has acertado los primeros 14 resultados. Y en este decimoquinto partido no solo tienes que acertar quien gana sino también el número de goles. Para cada equipo tienes que acertar los goles que marcará: 0, 1, 2 o más.
Este es un ejemplo real de lo que llamaremos una apuesta sencilla de quiniela (aquella en la que solo seleccionas una opción para cada partido). O también podemos llamarlo boleto.
El coste de las apuestas
Jugar un boleto con una apuesta sencilla como la de arriba cuesta 0.75€. También existe la opción de hacer apuestas múltiples. Es decir, añadir más de un pronóstico para algunos partidos. Por ejemplo, imagina que en el primer partido, Suiza-Austria, quieres marcar tanto la opción 1 como la opción 2 (es decir, solo fallarías si empatan). A esto se le llama un doble. Hacer esta apuesta cuesta más dinero. Concretamente el doble, 1.5€. En el fondo es como si jugaras dos apuestas simples, una marcando el 1 y otra marcando el 2.
En el ejemplo solo se ha usado un doble, pero puedes usar más. Incluso triples (marcar todos los posibles resultados asegurándote el acierto). No es más que una forma de evitarte tener que echar muchas apuestas sencillas. La cuestión es que por cada doble multiplicas el precio x2 y por cada triple x3.
Si juegas 2 dobles y 3 tiples la inversión sería de 81€:
Si quisieses jugar 14 dobles la inversión sería de 12.288€:
Los premios
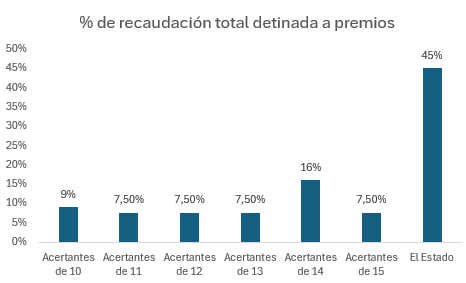
Llamaremos recaudación a la suma de todas las apuestas de todos los jugadores para una jornada dada. De entrada el Estado se lleva el 45% de la recaudación. Esto ya deja claro que en agregado es un juego de esperanza matemática negativa (o dicho más coloquialmente, un juego perdedor). No es ninguna sorpresa, todos los juegos organizados por el Estado lo son (salvo situaciones excepcionales). El gordo de Navidad es perdedor. El sorteo del Niño es perdedor. Y así casi con todo. Al final no deja de ser un mecanismo de recaudación.
La parte que no se lleva el Estado, el 55% de la recaudación, se reparte entre todas las personas que hayan acertado 10 o más partidos de la siguiente forma:
Por ejemplo, si hay 50 personas que han acertado 10 la forma de calcular su premio sería:
Esto tiene una implicación clave: no solo ganas en función de tus aciertos sino que depende también de cuantas personas han tenido el mismo número de aciertos que tú.
Hay algunas consideraciones menores que, si bien no son relevantes para seguir el post, no quiero dejar pasar
Si el premio es mayor a 40.000€, el estado también se quedará el 20% del importe por encima de 40.000€.
En el caso de acertar 15, el premio puede verse incrementado (respecto al cálculo explicado más arriba) si hay bote acumulado de otras quinielas pasadas.
Si tras calcular el premio, este es menor de 1€, no se cobra nada. Imagina que hay muchísimos acertantes de 10. Al repartir el 9% de recaudación entre muchos acertantes podría salir un premio menor de un 1€.
Para información más detallada puedes leer las reglas oficiales aquí.
2. Premisas clave de la metodología
Solo se enfoca en los 14 primeros partidos. Es decir, esta restringida a la rentabilidad que pueda generar el acertar entre 10 y 14 partidos. El posible incremento por acertar el pleno al 15 sería un extra de rentabilidad que no se ha modelizado. ¿Por qué?
Hace que la metodología sea conservadora en lo que a los cálculos de rentabilidad se refiere porque solo contempla parte de los premios.
Simplifica el problema en términos analíticos al eliminar una variable.
Simplifica el problema en términos computacionales. Al eliminar un partido del análisis el problema tiene una variable menos. Y eso se nota. Ya lo veremos más adelante.
Solo contempla hacer apuestas sencillas. Es decir, como si no existieran los dobles ni los triples. Pero sí contempla hacer varias apuestas sencillas.
Requiere como pilar fundamental conocer la probabilidad de cada posible resultado (victoria local, visitante, o empate) en cada uno de los 14 partidos.
Es decir, hay que alimentar la herramienta con 42 probabilidades (14 partidos multiplicado por 3 probabilidades para cada uno).
Estas probabilidades no las estimamos nosotros, las obtenemos de los operadores de apuestas deportivas (bet365, betfair etc). Ellos son los que tienen infinitos medios para hacer las estimaciones y tienen el incentivo correcto a hacerlo lo mejor posible.
Requiere conocer, para cada partido, que % de personas han apostado que gana el local (1), que gana el visitante (2) o que hay empate (X). Es decir, necesitamos saber cómo está apostando el resto de personas.
¿Por qué? Porque como hemos comentado más arriba, el premio no solo depende del número de aciertos sino de cuanta gente haya logrado el mismo números de aciertos. Por tanto, saber como está apostando el resto del mundo es clave.
Estos datos son públicos y los ofrece Loterías y Apuestas del Estado (a estos datos los llamaremos LAE).
Utilizamos La Web del Quinielista para hacer las apuestas de forma automática. Además es útil porque centraliza los datos LAE y las probabilidades reales de las casas de apuestas. Es decir que a través de esta web podemos obtener todos los datos.
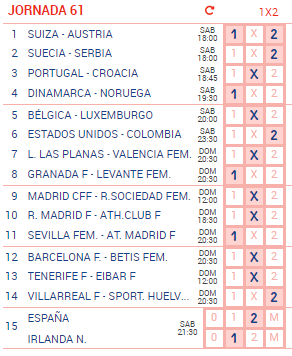
Más abajo puedes observar un ejemplo de los datos que necesitamos. Observa como en el séptimo partido hay una fuerte diferencia entre la probabilidad real de que gane L. Las Planas (51%, según las casas de apuestas) y el % de personas de personas que han apostado que ganará dicho equipo (35%, según Loterías y Apuestas del Estado).
La gente esta infravalorando las opciones de ganar de L. Las Planas. Y no nos importa el motivo. La cuestión es que estas situaciones generan oportunidades de arbitraje. Si una quiniela fuera muy obvia y fuese muy fácil acertar 14, todo el mundo acertaría, y a la vez todos perderían porque el premio se repartiría entre todos.
Hay situaciones en las que es posible apostar en contra de lo que está haciendo el resto de jugadores (y por tanto obtener un premio mayor si tienes el número suficiente de aciertos) y a la vez no penalizar tus probabilidades de acierto.
Tambien hay veces en las que seguir al rebaño puede ser buena idea, si la penalización en el potencial premio a ganar, se ve compensada por un incremento muy alto de la probabilidad de obtener un premio.
Al final es cuestión del balance entre probabilidad de obtener un premio y la cuantía del premio que obtienes en caso de salir premiado.
3. Análisis completo para encontrar la quiniela más rentable
Con todo este contexto ya podemos entrar en materia y tratar de encontrar el mejor boleto, o mejor combinación de 14 resultados (acuérdate que ignorábamos el decimo quinto partido).
Hay entre 4 y 5 millones de posibles boletos a jugar, en concreto:
¿Cómo elegimos el mejor de entre tantas opciones? Pues primero tenemos que decidir qué significa el mejor.
Nosotros definimos como mejor boleto al que tenga mayor premio esperado (PE).
Entendemos por premio esperado la multiplicación de la probabilidad de obtener el premio y la cuantía del premio.¡Ojo! Esta no es la única opción. Un ejemplo para ilustrarlo: imagina que te dieran la opción de jugar, una sola vez, a uno de estos juegos:
Un 90% de probabilidad de ganar 1.000€ → Premio esperado: 900€.
Un 0.1% de probabilidad de ganar 1.000.000€ → Premio esperado: 1.000€.
¿Qué elegirías? Si te dejases llevar solo por el premio esperado elegirías el 2. Sin embargo, probablemente tu cabeza te dice que el 1. Lo que está ocurriendo es que estás poniendo sobre la mesa (quizá sin ser consciente) el riesgo. En la segunda opción la probabilidad de que se materialice una ganancia jugando una sola vez es muy baja. O dicho de otra forma: es una rentabilidad muy volátil o con mucha varianza. En este caso, el incremental de premio esperado (+100€) no te compensa la volatilidad a la que te expones.
Seguramente tu respuesta cambiaría si te diera la opción de jugar al mismo juego un millón de veces. Es decir, cuando tienes un buen premio esperado te interesa que se repita el juego el máximo número de veces posible. De esta forma el efecto de la varianza se disipa al llevarte el juego al largo plazo.
Si te gusta la inversión probablemente esto te suene. Es conceptualmente similar al Ratio Sharpe, extensamente utilizado para valorar activos en base a su rentabilidad y riesgo.
La cuestión es que nosotros hemos decidido, de forma arbitraria, que el mejor boleto es aquel que tenga mayor premio esperado. Nos olvidamos de la varianza, al menos por el momento.
La idea entonces es sencilla: vamos a calcular el PE de todos los posibles boletos y nos quedaremos con el que tenga el máximo PE.
Cómo calcular el Premio Esperado
Existen 4.782.969 resultados posibles que pueden darse una vez elegido el boleto con el que jugar. Imagina que ordenamos todas las opciones ordinalmente y creamos una matriz en la que las filas representan el boleto que jugamos y las columnas la quiniela que termina saliendo en la realidad:
En la imagen, la cajita del cuadro de línea discontinua representa la hipotética situación en la que nosotros apostamos al boleto 2 pero finalmente el resultado real es el del boleto 4.782.968.
Nótese que el número de cajitas es diabólico → 4.782.968 x 4.782.968 Pues bien, para esa cajita concreta necesitamos calcular fundamentalmente 3 cosas:
¿Cuál es la probabilidad de que ocurra resultado?
Esto es fácil, solo necesitas las probabilidades de todos los posibles resultados para cada partido (que te recuerdo que lo extraemos de las casas de apuestas). De hecho este valor no depende de la fila de la matriz, solo de la columna en la que estamos.
¿Cuántos aciertos tendríamos?
Esto es trivial. Solo hay que comparar los pronósticos en el boleto 2 con los resultados obtenidos.
¿Cuál sería el premio para dicho número de aciertos?
Una vez conocemos el número de aciertos, solo necesitamos dos fuentes de información adicionales:
¿Cuántos apostantes hay? Esto es fácil estimarlo porque conocemos la recaudación total de la quiniela y el coste de jugar un boleto.
¿Qué están apostando los jugadores? Aquí es donde entran en juego los datos públicos LAE que ya comentamos más arriba.
Imagina que según los datos LAE en el primer partido de la quiniela el 100% de las personas han apostado que gana el equipo local. Entonces cualquier posible resultado en el que eso no ocurra tendrá, como mucho, premiados con 13 aciertos.
Aunque es un caso extremo, creo que permite intuir como el % de jugadores que apuestan a cada evento ayuda a estimar el número de aciertos que pueden tener.
En realidad el cálculo no es tan trivial porque falta cierta información. Conocemos el % de personas que apuestan al local, al empate y al visitante para cada uno de los partidos, pero no sabemos como se combinan entre ellos. Por ejemplo, podemos saber que el 20% de los jugadores apuestan a que gana el local en el primer partido y que el 20% de los jugadores apuestan a que gana el visitante en el segundo partido. Pero no sabemos si ese 20% es el mismo. Es decir, no sabemos si todos los que apuestan por el local en el primer partido apuestan por el visitante en el segundo. Esa información cruzada permitiría calcular con mucha más exactitud el número de acertantes para cualquier posible resultado y número de aciertos. Pero por desgracia, no existe.
En cualquier caso, con estos datos podemos obtener una aproximación razonable al premio que obtendríamos.
Resuelta una caja, la cuestión de repetir el proceso para cada posible resultado. Una vez lo tenemos ya solo tenemos que hacer un sumatorio:
Importante mencionar que en la mayoría de posibles resultados nuestro premio será 0 porque acertaremos menos de 10 partidos. Por lo tanto, para un boleto dado, no hace falta recorrer toda la fila, solo aquellas cajitas en la que tengamos 10 o más aciertos (cosa que ocurre en aproximadamente en 20.000 de los posibles resultados). Por tanto, la imagen sería más correcta así:
En cualquier caso, una vez calculado el premio esperado de un boleto, solo tenemos que seguir la misma operativa con todos los posibles boletos a jugar.
Conceptualmente no es un proceso muy complejo, pero computacionalmente puede ser retador. De hecho, la primera vez que resolvimos el problema completo siguiendo esta lógica lo hicimos utilizando los servicios Cloud de Amazon (AWS) para paralelizar el proceso lo máximo posible.
Pensamos que todavía tenemos mucho recorrido optimizando tiempos de cálculo. Si a alguien se le ocurre algún truco interesante que no dude en ponerse en contacto.4. Análisis Premio Esperado VS Probabilidad de Premio
Con el premio esperado calculado para todos los boletos, solo nos queda analizar resultados.
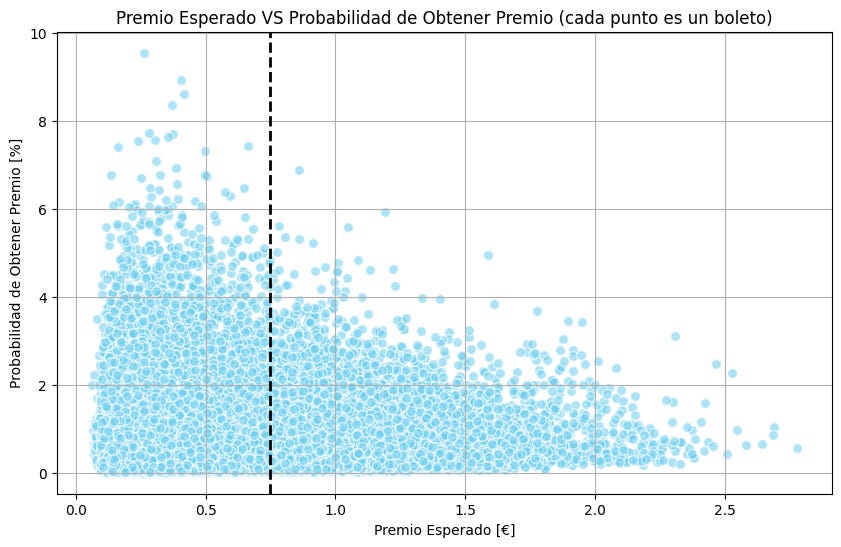
A continuación se grafican todos los posibles boletos en función de su premio esperado y su probabilidad de salir premiado (los resultados concretos varían de una jornada a otra pero las conclusiones del análisis se mantienen).
Solo los boletos con PE>0.75€ tienen sentido (ya que al menos queremos ganar lo que nos ha costado la apuesta). Es decir, solo los boletos a la derecha de la línea vertical negra son rentables matemáticamente. Solo el 15% de los boletos cumple esta restricción.
Hay boletos con PE>2€:
Si la apuesta son 0.75€, un PE=2€ equivale a una rentabilidad de 167%. No está mal.
El problema es que tienen probabilidades bajas de obtener premio (en torno al 0.5%).
Es decir, podemos elegir boletos con una rentabilidad muy alta pero que tienen una probabilidad de salir premiados muy baja.
Si en un año se juegan 70 quinielas y nuestra probabilidad de recibir premio en cada una de ellas es 0.5%, ¿Cuántas jornadas necesitamos para asegurarnos conseguir algún premio?
Jugando en torno a 30 jornadas hay un 80% de haber salido premiado alguna vez.
Pero claro, no solo es cuestión de obtener un premio. No es lo mismo salir premiado por acertar 10 que 14. Como te puedes imaginar lo primero es mucho más probable que lo segundo. Y por tanto estos resultados no quieren decir que tras 30 jornadas tengamos un 80% de posibilidades de ir en positivo.
En definitiva, que hay un problema de varianza que impide poder invertir fuertes cantidades ya que, aunque la estrategia sea matemáticamente rentable, te podría exponer a pérdidas enormes en el corto plazo. ¿Qué estamos haciendo entonces?
5. Implementación real a través de heurísticas
Llegados a este punto tenemos dos grandes problemas que mitigar:
Apostar al boleto más rentable nos expone a una varianza excesiva.
Resolver el problema de forma completa (como se ha expuesto en la sección anterior) es computacionalmente exigente y no podemos hacerlo de forma recurrente.
La solución, parcial, a ambos problemas se basa en dos frentes:
Calcular en boleto con mayor PE en base a una heurística, sin tener que resolver el problema completo.
Apostar a más de un boleto en base a otra heurística.
Heurística para encontrar el mejor boleto
Para poder detallar la heurística antes tengo que explicarte un concepto llamado distancia, que no es más que el número de pronósticos diferentes entre dos boletos. Por ejemplo estos dos boletos están a distancia 1 porque solo difieren en el pronóstico de un partido (el primero en este caso).
Ahora ya podemos ver el proceso:
Seleccionamos un boleto aleatorio como primer candidato a ser el boleto con mayor PE.
Calculamos el PE de los 28 boletos que están a distancia 1 de nuestro candidato.
Si entre los 28 boletos hay alguno con mayor PE que nuestro candidato, este nuevo boleto pasa a convertirse en el candidato. Y volvemos al punto 2.
En caso contrario, mantenemos candidato, y pasamos a calcular el PE de los 364 boletos que están a distancia 2 de nuestro candidato.
Si entre los 364 boletos hay alguno con mayor PE que nuestro candidato, este nuevo boleto pasa a convertirse en el candidato. Y volvemos al punto 2.
En caso contrario, mantenemos candidato, y pasamos a calcular el PE de los 2.912 boletos que están a distancia 3 de nuestro candidato.
Si entre los 2.912 boletos hay alguno con mayor PE que nuestro candidato, este nuevo boleto pasa a convertirse en el candidato. Y volvemos al punto 2.
En caso contrario, el candidato es el boleto con mayor PE de todos los posibles boletos.
Esta heurística, tras más o menos 8 iteraciones, llega al mejor boleto. Como realmente no hemos comparado con todos los posibles boletos no tenemos garantía 100% de que sea el mejor de ellos, pero en los casos en los que hemos comparado con la resolución del problema completo la solución ha coincidido.
Fíjate que en este caso no analizamos los más de 4 millones de boletos. Solo una pequeña parte. Cada iteración, como mucho, te exige calcular el PE de unos 3.300 boletos (cosa poco frecuente además). Si hacemos unas 8 iteraciones esto nos lleva a calcular, en el peor de los casos, unos 26.000 boletos (un 0.55% del problema completo).
Heurística para disminuir la varianza
Parece claro que para disminuir la varianza de forma significativa habría que buscar alguna estrategia para apostar a más de un boleto simultáneamente. Es un sacrificio de rentabilidad esperada a cambio de mayor probabilidad de salir premiados.
Imagina que nos planteamos apostar a dos boletos. ¿Cuáles serían los adecuados? Podríamos coger los dos boletos con mayor PE. Pero nada garantiza que eso sea lo mejor. Esos dos boletos podrían ser muy parecidos (distancia 1) y por tanto salir premiados casi de forma equivalente.
Podría pasar que la mejor combinación de dos boletos no incluye la mejor boleto de forma individual. No lo sabemos.
Nuestra aproximación a este problema ha sido la siguiente:
Calculamos el mejor boleto (con la heurística ya explicada en la sección anterior). Este es nuestro boleto jugado número 1.
Calculamos el mejor boleto a distancia 3 del boleto jugado número 1. Este es nuestro boleto jugado número 2.
Calculamos el mejor boleto que esté a distancia 3 de los dos boletos anterior. Este será nuestro boleto jugado número 3.
Calculamos el mejor boleto que esté a distancia 3 de los tres boletos anterior. Este será nuestro boleto jugado número 4.
De esta forma buscamos jugar 4 boletos de alto valor y que no estén muy solapados entre ellos de forma que abarquen un mayor universo de posibles resultados y se aumente la probabilidad de salir premiado.
6. Resultados tras 51 jornadas probando la estrategia
El primer resultado, aunque no económico, es que es una inversión 100% pasiva. Esta todo automatizado.
Gracias a Google Sheet (dónde están implementadas las heurísticas) y Telegram (donde tenemos un bot que nos informa de cómo van los resultados) nuestra única tarea es esperar a ver qué pasa y seguir pensando en como afinar la metodología.
La estrategia lleva operando 51 jornadas. Más por diversión que por otra cosa ya que, aunque tenemos confianza en la metodología, la varianza todavía no es tan baja como nos gustaría.
En cualquier caso, los resultados son:
Se juegan 4 boletos por jornada → Dinero invertido 51*3€=153€
Premios obtenidos:
1 x 10 aciertos → 4.56€
3 x 11 aciertos → 12.62€
1 x 12 aciertos → 44.70€
Es decir, que de momento vamos 91.12€ abajo.
Puedes auditar los resultados en la web de nuestra peña, tuiterquinielas.El punto positivo es que el número de veces que hemos obtenido premio y las cantidades premiadas encajan bastante con nuestras metodologías de cálculo.
No obstante, seguimos teniendo el gran problema de la varianza. Con la estrategia actual la probabilidad de estar en positivo tras un número n de jornadas es la siguiente:
No es de extrañar que tras 51 jornadas estemos en pérdidas. Las probabilidad de estar en positivo es solo de un 17%.
El lado positivo es que la línea es ascendente. El largo plazo nos debería llevar a la rentabilidad, aunque más lento de lo que nos gustaría.
Con todo esto, ya te puedes imaginar que nuestra investigación está yendo en la dirección de impactar en esta última gráfica para tratar de hacer el largo plazo algo más corto y así poder invertir cantidades más significativas sin someternos a tanta varianza.
Sabemos que esto pasa inexorablemente por aumentar el número de boletos apostados por jornada pero todavía no hemos dado con la tecla de cuales elegir para disminuir la varianza de forma significativa.
Seguiremos informando.
Muchas gracias por leer Ochenta Veinte!
Si te ha aportado valor y quieres más, puedes suscribirte aquí:
Y si ya eres suscriptor y quieres echarme una mano, puedes compartir el post:
Hasta la próxima
Álvaro OPK