La moneda trucada
Preguntaba ayer @sergibenet lo siguiente.

Tengo un post pendiente sobre frecuentistas y bayesianos. Pero lo veo prematuro, no me siento con fuerzas (ni conocimiento). Así que me voy a limitar a exponer mi punto y tocar las narices un poco.
La cuestión
Nadie en la historia ha visto salir 99 caras seguidas en una moneda justa. Ni lo verá. Es extremadamente improbable. Ni aunque estemos tirando monedas toda la historia del universo.
De la misma manera, las monedas trucadas son poco frecuentes. Yo no he visto ninguna y supongo que prácticamente el 100% de monedas que han existido son monedas justas.
Así que estamos ante un suceso difícil de explicar. ¿Cómo han podido salir 99 caras si las monedas trucadas no existen y con monedas justas es imposible?
Bueno, la cosa es que eso es lo que ha ocurrido. Y la cuestión no es qué probabilidad tenía eso de ocurrir sino si, una vez ocurrido, es más probable que venga de monedas justas (prob_apriori_justa*0,5^99) o de monedas trucadas (prob_apriori_trucada*1^99). En ambos casos estamos multiplicando casi 1 por casi 0, pero por pequeña que consideremos la probabilidad a priori de moneda trucada, ese casi 0 será seguro más grande que el 0,5^99.
Ejemplo 1
Cambiemos un poco el problema.
Hay 2 monedas en una caja negra. Una sabemos que es justa porque la hemos tirado previamente un millón de veces. La otra tiene 2 caras.
Sergi, utilizando la moneda justa, elige al azar una de las 2 monedas. Una vez elegida la tira 2 veces. Las 2 veces sale cara. ¿Cuál es la probabilidad de que a la 3ª salga también cara?
Pues de cada 200 veces que Sergi repita el experimento, 100 cogerá la moneda trucada y 100 la moneda justa. De las 100 que coja la moneda trucada las 100 sacará 2 caras. Y de las 100 que coja la moneda justa 25 sacará 2 caras.
Pero ya sabemos que han salido 2 caras. Así que podemos decir que en 100 de cada 125 veces que ya hayan salido 2 caras será porque es la moneda trucada y solo en 25 de cada 125 veces será porque es la moneda justa.
Por tanto
tenemos una probabilidad del 80% (100/125) de estar ante la moneda trucada en cuyo caso volverá a salir cara.
tenemos una probabilidad del 20% (25/125) de estar ante la moneda justa en cuyo caso volverá a salir cara la mitad de las veces.
Así que la probabilidad de que vuelva a salir cara es el 90% (80%*100%+20%*50%).
Ejemplo 2
Repitamos el problema pero cambiando la caja negra. En lugar de 2 monedas ahora hay 100 y solo 1 de ellas está trucada. Este enunciado es quizá más parecido a lo que pensamos cuando vemos una moneda: no descartamos que pueda estar trucada, pero es muy improbable. Lo normal es que las monedas sean justas. Al menos así son las que nos hemos encontrado en el pasado...
Pues bien, con este cambio y haciendo igualmente 2 tiradas en las que sale cara, repetimos el análisis.
El resultado es que solo el 3,88% de las veces que salen 2 caras estamos ante la moneda trucada. Por tanto la probabilidad de que vuelva a salir cara se reduce a poco más del 50% (51,94%).
Ejemplo 3
Por último, pongamos que sigue habiendo 100 monedas en la caja negra solo 1 trucada, pero en lugar de 2 caras seguidas sacamos 10.
Pues en este caso se vuelve a igualar la cosa. La probabilidad de que estemos ante la moneda trucada es del 56% y por tanto la probabilidad de volver a sacar cara sube hasta el 78%.
Una pregunta que nos podríamos hacer en este punto es la siguiente. Si en lugar de 10 sacamos 99 caras seguidas, ¿cuántas monedas necesitaríamos en la caja negra para que sea igualmente probable estar ante la trucada que ante una moneda justa? Pues necesitaríamos que en la caja negra hubiera 1 moneda trucada por cada 6*10^29...
La caja negra
Lo que en los ejemplos anteriores hemos llamado "caja negra" es la distribución a priori, el cómo ha sido seleccionada la moneda. Aquí lo hemos explicitado y definido pero en realidad es una información que nunca vamos a tener.
Y la caja negra es en el fondo la clave de todo. Ya hemos visto que la probabilidad a priori influye muchísimo en el resultado.
Esto por cierto me recuerda al famoso problema de una enfermedad muy infrecuente y un test muy fiable. Sí, el test falla poco pero si le haces el test a toda la población, dado que la enfermedad es muy poco frecuente, podría haber más falsos positivos que positivos verdaderos. En este caso, la presencia de la enfermedad a priori (cómo lo sabemos?) es la caja negra.
Por tanto, ¿qué ocurre con los problemas anteriores si no sabemos qué hay dentro de la caja negra? No sabemos ni cuántas ni cómo son las monedas que hay dentro. Pues que nos toca inventarnos.
Creo que la forma más razonable de "inventarse" es considerar por defecto que todo son sucesos equiprobables. No tenemos ninguna información para primar un suceso sobre otro. Es decir, en nuestro caso, la caja negra contiene monedas con sesgos uniformemente distribuidos entre 0 (siembre sale cruz) y 1 (siempre sale cara). Es igual de probable que se haya seleccionado una moneda con una probabilidad de cara del 20%, del 50% o del 100%.
Y esta sería la probabilidad de que salgan 99 caras seguidas en función del sesgo de la moneda.
Y como hemos asumido que cualquier sesgo es equiprobable, el área bajo la curva será la frecuencia con la que salen 99 caras seguidas. Sorprendentemente, con una moneda seleccionada de esta manera (entre monedas con sesgo uniformemente distribuido) la probabilidad de sacar 99 caras seguidas es del 1% (integral entre 0 y 1 de x^99).
Pero lo que queríamos saber es cuál es la probabilidad de que en la siguiente tirada salga cara. Bueno, pues si tenemos cuál es la probabilidad de que la moneda tenga cada sesgo concreto, la multiplicamos por el propio sesgo y las sumamos todas; nos sale el resultado. Si no me he equivocado en los cálculos, la probabilidad de que en la siguiente tirada salga cara es de 100/101.
Discusión de asunciones
Hay quien dirá que esto no es así, que cuando se dice "moneda" debemos asumir que es una moneda con un sesgo de 0,5. A mí esto me parece problemático por dos motivos.
El primero es porque convierte el problema en una tautología. El enunciado te estaría diciendo que hay una moneda que tiene un sesgo de 0,5, luego una frase irrelevante, y luego te preguntaría cuál es el sesgo de la moneda.
Si tiramos una moneda cuya probabilidad de cruz es del 50% (...) ¿cuál es la probabilidad de que (...) salga cruz?
Pero sobre todo me parece problemático porque no es lo que ocurriría en la vida real. En la vida real las probabilidades 0% y 100% apenas existen. Se reservan casi exclusivamente para sucesos lógicamente imposibles o mal construidos. Pero todos concebimos que puedan existir, aunque sean poco frecuentes, monedas trucadas, monedas con dos caras, monedas con pesos en un lado... Y desde luego si experimentamos una situación que es extremadamente improbable, como que salgan 99 caras seguidas, sospecharemos que estamos ante una de esas monedas.
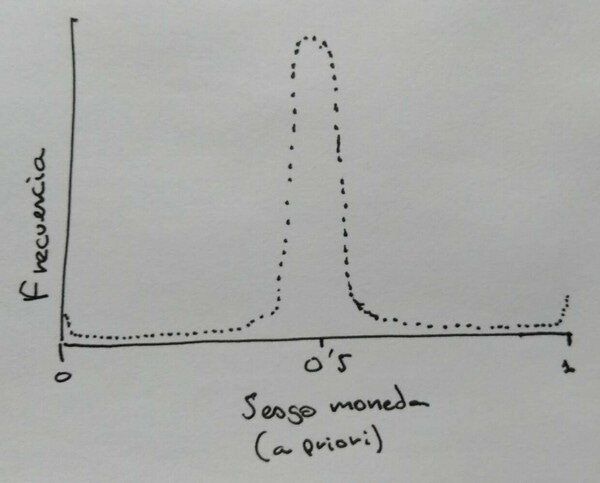
También hay quien podría argumentar que la asunción que he utilizado yo de sesgos a priori uniformemente distribuidos entre 0 y 1 tampoco es realista. Y estaría de acuerdo con ellos. Cuando nos hablan de "una moneda" tendemos a pensar que la mayor parte de monedas se concentran en el sesgo 0,5 y que son muy poco frecuentes los sesgos extremos.
De hecho si yo me enfrentara al problema en la vida real intentaría repetir este análisis definiendo primero cuál me parece que es la distribución de sesgos a priori más razonable. Probablemente pensaría en una distribución parecida a una normal con una gran montaña en el 0,5. Y luego esa distribución la modificaría con algunos razonamientos que pueda hacer como que me parece más probable que una moneda pueda tener un sesgo de 1 o de 0 que de 0,95 o de 0,05 (porque me resulta más sencilla la manipulación de ponerle directamente dos caras o dos cruces que la de conseguir que salga cara un 95% de las veces que no tengo muy claro cómo podría físicamente conseguirse eso).
De la misma manera intentaría plantearme en qué situación estoy, si estoy en un circo, si estoy ante un mago, si estoy ante un timador ambulante, si estoy en un casino... y pensaría en cómo ha podido ser seleccionada esa moneda. Es algo muy subjetivo pero quizá podría intentar justificarlo buscando una muestra similar a la situación en la que me encuentre: cuántas monedas se han tirado en casinos, cuántas han resultado ser trucadas, cuántas monedas de este grosor están trucadas, etc...
Por tanto si en la vida real ya nos costaría encontrar esas métricas para justificar nuestras estimaciones subjetivas de probabilidad a priori, considero que en un problema ficticio la única respuesta posible es "cuéntame de dónde ha salido esa moneda" o simplemente "define moneda".